什么是期权调整价差
期权调整价差(OAS)是相对无风险利率的价差,通常以基点(bp)的方式进行量度。一般以国债即期利率曲线(或同一发行人即期利率曲线)为基准,在此基准上水平浮动一定利差,综合考虑利率的波动,将期权调整后的现金流进行贴现,得到含权债券的理论价格,最终使理论价格等于市场价格的利差水平就是OAS。OAS 可视为对投资者面临多种风险的补偿(例如流动性溢价、违约风险、模型风险)。
20世纪80年代随着抵押贷款支持证券(MBS)等含权债券市场规模的不断扩大,国际市场上出现了一种新的债券价值判断方法:期权调整利差option adjusted spread,简称OAS。由于OAS 综合考虑了即期利率曲线、利率波动、期权等因素,能够比较准确地反映利率敏感型固定收益证券的价值,因此被广泛运用于抵押贷款支持证券MBS、资产支持证券ABS、结构性证券(structure)、保险产品等各种含权债券的价值分析中。
期权调整价差的作用
透过OAS 我们可以得到以下信息:
1、含权债券的期权成本。含权债券价值可以分拆为两部分:普通债券价值和期权价值。在其它条件相同的情况下,通过含权券与普通券的比较我们可以得出期权的市场价值:
期权价值(以利率基点的形式)=静态价差-OAS
Option value(in basis point)=static spread-OAS
2、投资者的风险补偿。OAS是对投资人所承受的信用风险、流动性风险以及其他风险的补偿。例如在其他条件相同的情况下,对于含发行人赎回权(callable)的债券,发行人拥有随时赎回的看涨期权,持有人面临因债券赎回而导致的再投资风险以及价格压制风险(负凸性)。值得注意的是,由于OAS 所体现的是期权移除价差,在其他条件相同的情况下,所体现的的风险补偿应该与普通债券静态价差体现的风险补偿(信用风险、流动性风险等)近似。)
3、价格敏感性分析。由于现金流的波动,修正久期和凸性测量公式失效。通过OAS 计算,利用有效久期(effective duration)和有效凸性(effective convexity)能够较好量度含权债券价格相对利率变化的敏感度。具体是将OAS 固定,上(下)移动即期利率曲线,调整现金流并贴现得出新的债券价格。有效久期与有效凸性公式如下:
有效久期=
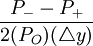
;有效凸性=
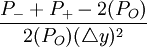
其中
P − 表示利率上涨后的价格、
P + 表示利率下跌后的价格、
PO表示初始价格、 Δy表示变动的利率。
4、新产品定价。利用市场OAS 信息为新发行的含权债券定价。
5、投资品种的选择。比较信用等级、债券条款以及期权条款相同的含权债券间的OAS,选择OAS高的品种进行投资。
OAS一般计算过程
首先,找出作为OAS 比较的基准利率-即期利率曲线。从理论上讲,即期利率曲线应由不同期限的一系列零息券利率所组成,但是市场零息券数量有限、期限不全,因此实际操作过程中通常是利用现有债券,运用票息剥离法(bootstrap)以及线性插值法或其他统计方法得到即期利率曲线。
其次,以适当的模型刻画利率变动过程。一般认为利率是遵循正态随机游走或对数正态随机游走过程。假设利率的波动率水平,选择适当的模型随机产生利率并使之与即期利率期限结构相一致。
三,沿每一条利率路径,依据契约条款,计算每个时间节点的自由现金流。
四,在基础利率水平上加上一定利差(OAS)作为贴现率,将自由现金流依利率路径贴现,形成零时刻的价值。
五,将零时刻各利率路径的贴现值加权,得到含权债券的模型理论价值。
最后,重复第四、五步使得理论价值等于市场实际价格,解出OAS。
">编辑] 期权调整价差模型的实际运用
国开行是中国债券市场创新的急先锋,其发行的金融券不论从发行规模、发行数量还是交易量都仅次于国债,在银行间债券市场颇有影响力。截至2004 年9 月,国开行在银行间债券市场共发行含权债券17 只,上市15 只(合并上市两只)。其中含发行人赎回权(callable)的债券5 只,含持有人回售权(puttable)的债券6 只以及含持有人换券权(exchangeable)债券4 只。试图运用OAS 分析方法,对市场较为认同的国开行含权债券以及新券定价进行分析。
(一)样本选择
以04 国开11(6 月30 日发行)为定价对象,选取6 月29 日债券市场交易数据。并选择2004 年6 月22 日至6 月29 日有交易记录的的含权券作为比较样券。
表一 样本概况
(二)模型建立
1) 由于银行间成交不活跃,以6 月29 日上海交易所国债交易数据,运用票息剥离法和线性插值法生成国债即期利率曲线。其中1 年期即期利率水平为2.73%、3 年期即期利率水平为3.64%、5 年期即期利率水平为4.387%、10 年期即期利率水平为4.763%。
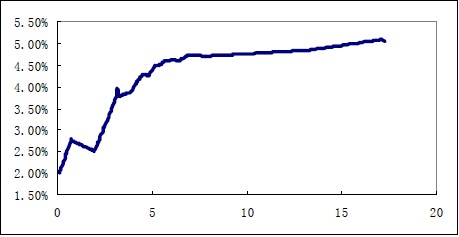
ngdesc="/wiki/Image:6%E6%9C%8829%E6%97%A5%E4%BA%A4%E6%98%93%E6%89%80%E5%9B%BD%E5%80%BA%E5%8D%B3%E6%9C%9F%E5%88%A9%E7%8E%87%E6%9C%9F%E9%99%90%E7%BB%93%E6%9E%84.jpg" />
2)其次选取HO-LEE 的对数模型为基础构建利率二叉树:
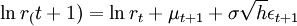
。
其中h 指时间间隔、\mu_{t+1}指T+1时刻利率的对数漂移率、σ是利率的年化波动率、\epsilon_{1+t}服从标准正态分布的白噪声。设定利率上升的概率为1/2, 下降的概率1/2 , 通过Black-Derman-Toy 对HO-LEE 模型变形:。
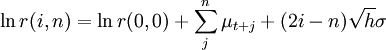
。
其中(i,n)表示一种状态,i 是自初始时刻上升(up moves)数量,n 表示自初始时刻的阶段数。通过模型我们可以知道在第n 个阶段,(i,n)状态的利率与(0,n)状态的利率存在以下关系:。
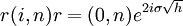
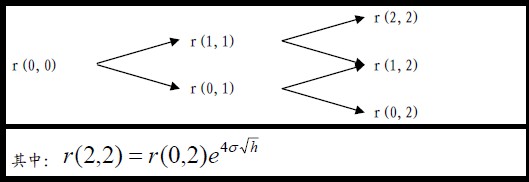
ngdesc="/wiki/Image:%E5%9B%BE%E4%BA%8C-BDT_%E6%A8%A1%E5%9E%8B%E4%BA%8C%E5%8F%89%E6%A0%91%E6%A8%A1%E6%8B%9F.jpg" />
结合状态价格Q(i,n)与第n阶段即期利率y^n的关系(n>0):
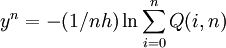
即
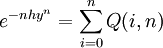
运用递推的方法得到各阶段各状态的利率r(i,n),构成基准利率二叉树。例如假设h=1得到图三。
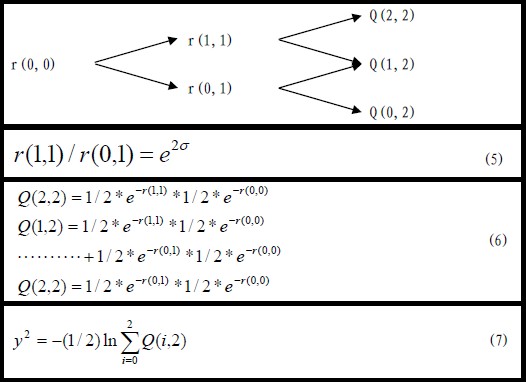
ngdesc="/wiki/Image:%E5%9B%BE%E4%B8%89%EF%BC%9A%E5%88%A9%E7%94%A8%E7%8A%B6%E6%80%81%E4%BB%B7%E6%A0%BC%E9%80%92%E6%8E%A8%E5%88%A9%E7%8E%87%E4%BA%8C%E5%8F%89%E6%A0%91.jpg" />
3)假定年利率波动率为45%。根据交易所国债696 的日交易数据换算日收益率,用收益率对数差分求波动率,将波动率乘以\sqrt_{240}得到年化波动率。
4)在基准利率二叉树的基础上,加上一定利差(OAS)得到新的利率二叉树。
5)从后向前将现金流逐期贴现,调整OAS 使得贴现值与市场价格相等。
(三)结果分析
受升息预期以及国债回购事件的影响,2004 年上半年在国债的带动下债券市场历经了一轮暴跌,6 月末市场开始止跌但市场人气依旧涣散成交不活跃,各期限品种地券价仍在调整。通过上述模型分析具体表现如下:
(1) 总体来看,国开行金融券与国债间的利差水平不大。由于国开行为国家政策性银行,信用由国家“隐性”担保,违约风险不大;二级市场交易也相对活跃,流动性溢酬较少;而且短期内国债仍有市场风险,因此国开行金融券与国债间的利差水平不明显。具体模型表现是:普通的国开行金融券与国债间的静态价差较小。
表二:2004 年6 月29 日普通国开行券与国债的静态价差
(2) 不同期限间国开行与国债的利差水平略有不同。通过表二可以看出中短期限国开行券的静态利差为负值,这表明中短期限国债品种价格仍在调整中,而金融债相对来说短期市场风险小、市场要求收益率水平较低。中长期限品种间的利差水平较为合理,表现在国开行券较国债的静态价差为正值,说明市场对中长期限品种的收益水平较为认同。
(3) 含权债券的价值尚未充分体现。表三中的含权券赋予了持有人或者提前回售或者调换为浮息券的的权利,持有人对含权券的要求收益水平应该比普通券的低,但结果表明无论期限长短,含权券的期权调整价差全部为正值,且含权券的OAS与可比较普通券的静态价差相比明显偏高,与理论相悖。尤其是03 国开22 全价仅为98.865 元,而其距离可调换日不到2 个月,可调换的浮息券01 国开08净价却维持在面值100 元。这些说明现阶段债券市场对含权券的价值仍未充分认识,含权券的价值被低估。
表三:2004 年6 月29 日含权国开行券与国债的期权调整价差
(4) 结合市场环境,我们以国债即期利率期限结构为基准向上浮动不超过1bp,为04 国开11 定价。模拟结果如下:
表四:04国开11定价表
04 国开11最终招标结果为票面利率4.2%,模型测算期权调整价差为0.81 个基点(BP)。
(四)模型的不足
首先银行间市场流动性不足导致价格信号失真,模型分析可能有偏差。
其次波动率的选择对定价结果影响较大,由于数据获取手段有限,只能根据短期国债利率696 数据统计,结合市场趋势粗略估计利率的波动率。
第三,二叉树选取步数选择较少,可以根据实际需要增加二叉树步数以及利用三叉树提高模型精度。
参考文献
- ↑ 贺涛,陈蓉.期权调整价差(OAS)估值模型对含权债券定价的运用

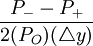 ;有效凸性=
;有效凸性=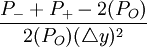
 ngdesc="/wiki/Image:6%E6%9C%8829%E6%97%A5%E4%BA%A4%E6%98%93%E6%89%80%E5%9B%BD%E5%80%BA%E5%8D%B3%E6%9C%9F%E5%88%A9%E7%8E%87%E6%9C%9F%E9%99%90%E7%BB%93%E6%9E%84.jpg" />
ngdesc="/wiki/Image:6%E6%9C%8829%E6%97%A5%E4%BA%A4%E6%98%93%E6%89%80%E5%9B%BD%E5%80%BA%E5%8D%B3%E6%9C%9F%E5%88%A9%E7%8E%87%E6%9C%9F%E9%99%90%E7%BB%93%E6%9E%84.jpg" />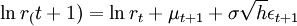 。
。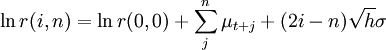 。
。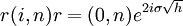
 ngdesc="/wiki/Image:%E5%9B%BE%E4%BA%8C-BDT_%E6%A8%A1%E5%9E%8B%E4%BA%8C%E5%8F%89%E6%A0%91%E6%A8%A1%E6%8B%9F.jpg" />
ngdesc="/wiki/Image:%E5%9B%BE%E4%BA%8C-BDT_%E6%A8%A1%E5%9E%8B%E4%BA%8C%E5%8F%89%E6%A0%91%E6%A8%A1%E6%8B%9F.jpg" />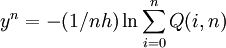
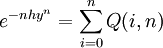
 ngdesc="/wiki/Image:%E5%9B%BE%E4%B8%89%EF%BC%9A%E5%88%A9%E7%94%A8%E7%8A%B6%E6%80%81%E4%BB%B7%E6%A0%BC%E9%80%92%E6%8E%A8%E5%88%A9%E7%8E%87%E4%BA%8C%E5%8F%89%E6%A0%91.jpg" />
ngdesc="/wiki/Image:%E5%9B%BE%E4%B8%89%EF%BC%9A%E5%88%A9%E7%94%A8%E7%8A%B6%E6%80%81%E4%BB%B7%E6%A0%BC%E9%80%92%E6%8E%A8%E5%88%A9%E7%8E%87%E4%BA%8C%E5%8F%89%E6%A0%91.jpg" />